Calibrating my torque wrench

A couple of weekends ago I managed to damage the thread on the crank axle bolt of my XTR M9100 chainset.  It was really annoying, partly because I had a bike race the next day, but mainly because I felt it start to fail at a torque that was below Shimano's recommend torque setting of 45-55 Nm.  The bolt gave me that tell-tale sign of a problem, where it starts to turn more than it should, and without the resistance increasing in the way it should. This happened before my torque wrench was able to click when set to 42Nm, below the recommended torque setting.

I got a replacement bolt, but it made me wonder whether my torque wrench was badly calibrated.  It's a really cheap torque wrench, a budget Silverline torque wrench, bought from Toolstation, so it's quite possible that it's badly calibrated.

Anyway, I decided to use my workbench vice and hang a weight off the torque wrench, at several torque settings, then see at what distance (moment arm) the weight has to be at to cause the torque wrench to click.

The results, plotted below, shows that my torque wrench clicks out at a slightly lower torque than indicated on the wrench.  This means that it's safe, in that it won't over-torque a bolt. It means that the reason my XTR chainset bolt got threaded is a bit of a mystery, but it's probably because the Shimano bolt was faulty, rather than an issue with my torque wrench.

28 Nm on wrench

260mm with 10.15kg (99.57N)

= 25.88 Nm applied

36 Nm on wrench

320mm with 10.15kg (99.57N)

= 31.86 Nm applied

42 Nm on wrench

370mm with 10.15kg (99.57N)

= 36.84 Nm applied

46 Nm on wrench

402mm with 10.15 (99.57N)

= 40.03 Nm applied

Weight comparison for my mountain bikes

Weight is not the most important consideration when it comes to cycling performance, as discussed previously in one of my older blog posts.

Having said that, I still weigh the components of my bikes whenever it's convenient to do so.  By doing that, it gives me the information to know whether it'd be good value for money, or not, to upgrade a component, or swap something over from one of my older bikes.  Nevertheless, it's not something I pay a large amount of attention to these days, having understood how important (or rather how not important) bike weight is on cycling performance. Still, it remains slightly interesting to me, hence this comparion.

I recently bought a Specialized Epic Evo as a new full suspension mountain bike.  I already own a 14-year old first generation 26 inch-wheeled Giant Anthem full suspension MTB and a Scott Scale 29-inch wheeled hardtail MTB.  I thought it would be interesting to compare the weights.  For all of the bikes, I've made some improvements to make them lighter, prioritising the items that would provide the best value for money (best gram saved per £).

Perhaps not surprisingly, the carbon-framed Scott Scale hardtail is the lightest of the three.  Most of the difference is coming from the frame, obviously, but I'm also running SRAM XX1 carbon cranks on it, and these are a fair bit lighter than the alloy Shimano XTR cranks on the other two.

What's most interesting is that my Giant Anthem is lighter than the Specialized Epic Evo, despite having an alloy frame, alloy wheels, and a triple chainset (versus the Epic's carbon frame & wheels, and 1x transmission).  Although the Anthem's wheels are on 26", which helps, I think it still shows that alloy wheels can be very light. The 3x9 transmission of the Anthem is also almost as light as the Epic's, despite the hefty triple crankset, but this is helped by the 11-32 XTR cassette, which is about 60% of the weight of the Epic's enormous 11-52 cassette.

Finally, the other big difference comes from the Epic's dropper post, and the Epic is the only bike that has a dropper.  That alone adds about half a kg.

Despite all this, I'm happy with the Epic's build and 10.9kg (23.9lb) total weight.

The benefits of unlocking Zwift's rear disc wheel

Today I got to Level 35 in Zwift, which that means I was able to get the Zipp Super 9 rear disc wheel.

It looks better on any Time Trial (TT) bike, of course (if you care about such things for your Zwift avatar!).  However, I wanted to know how much faster it is.  This post explains my calculation to determine just that.  The quick answer, if you don't want to read the full post, is 2.5 Watts.

I've been using Zwift since September 2015, which was not long after the launch of Zwift.  I'm not a massive fan of Zwift, I must admit, but I quite like it and I use it for a few months every year to help take some of the monotony out of winter indoor riding.  It's taken me that long time, about eight years, to get enough XP to get up to level 35 (approximately 5,700 Zwift miles).

Fastest Zwift Wheels

When talking about the fastest wheels in Zwift, it is worth clarifying that this applies only to wheels on TT bikes.  Why?  Because once you unlock the Zwift Concept Z1 road bike (aka the 'Tron bike'), then all other road bikes are slower, with a few caveats, regardless of the wheelset you put on them. See this Zwift Insider post for more information about that.

TT bikes are different though, and will always be faster than a road bike, including the Tron bike, when riding solo or in a no-draft TT event.

Zwift Insider's analysis

The guys at Zwift Insider do an excellent job of analysing bike and equipment choices within Zwift, amongst other things.  Their post here explains the fastest TT wheels, using their testing protocol, whereby they recorded the time required to ride the Tempus Fugit route (17.4km / 10.7miles) twice at 300W.

As shown in the table to the left, the faster wheelsets provide larger time savings.  However the fastest wheelset can only be unlocked at the higher levels within Zwift.

For some years, since Level 13, I've been using the Zipp 808 wheels on the TT bike, which are the fastest wheels for people at lower Zwift levels.  Now having the Zipp Super 9 disc wheel on the back, saves me 9 seconds on that 2 x Tempus Fugit route, versus two 808s, according to the Zwift Insider table above.  Given that the entire route takes "approximately 50 minutes" when ridden at 300W, then 9 seconds doesn't sound like very much!  In fact, the time/speed improvement is only 0.3% (9 seconds divided by 3000 seconds).

What I wanted to calculate is how much that time saving equates to, in terms of power savings and CdA reduction.

Important: As with all power saving values, it's crucial to keep in mind the associated speed, which in this case was 41.52 kph (25.79 mph), because any power savings due to aerodynamic changes are proportional to speed cubed.  Beware anybody that quotes power savings without also giving the associated speed!

CdA and Watt savings

I used my performance modelling spreadsheet (described here) to model the Zwift Insider test, where they completed two laps of the Tempus Fugit route at 300W, for a 75kg rider, in about 50 minutes, as shown below:

In addition to the parameters above, I had to make a few other assumptions to calculate the CdA, and these are simply guesses, because I don't know what assumptions Zwift makes.  I'm confident, however, that the power and CdA increments won't be particularly sensitive to this choice of conditions:

• Air pressure = 1012.5 bar (i.e. sea level pressure using the International Standard Atmosphere, ISA, conditions).
• Air temperature = 15 degrees C (i.e. sea level ISA conditions).
• CRR = 0.004 (which ZwiftInsider says here is the CRR that Zwift assumes for the road).
• Bike weight = 9kg
• Drivetrain losses = 2.5%

Using these assumptions, I calculated the baseline CdA to be 0.2710 m^2.  Then, by increasing the speed by 0.3%, giving a 9 second time saving, I calculated:

Either: 0.0025 m^2 CdA improvement (0.2710 -> 0.2685, or a 0.92% CdA reduction) at the same 300W power to achieve that 9 second saving.

Or: 2.5 Watt power saving at 41.52 kph (0.83% power saving) for the same 50 minute time, with that reduced CdA of 0.2685.

I think these numbers, especially the power saving, can be understood more intuitively by the average person.  A 2.5 Watt power saving is not large, but is not negligible either.

Are the numbers valid also for me?

Finally, I also wanted to check whether these values are valid for me, because I'm a slightly smaller and less powerful rider than was assumed by Zwift Insider.

Firstly, I calculated my CdA to be 0.2415, for my Zwift time trial bike using Golden Cheetah.  This is relatively easy to do (compared with real life), because in Zwift there is no braking, no wind and no other vehicles to mess things up!

Something to note is that my Zwift CdA is about 10% lower than the CdA for the Zwift Insider analysis, and this will be because I'm probably shorter (at 5 foot 10 inches) and slightly lighter (at 73 kg) than for the Zwift Insider study, and we know that Zwift adjust the CdA based on weight and height.

Next, I applied this CdA to my spreadsheet analysis.  Interestingly, for a 50 minute time to complete the 2 x Tempus Fugit distance, the power requirement was 270.6W, which is approximately what I could hold for 50 minutes, so I didn't adjust it any further.  Then, I reduced the CdA by the same 0.0025 m^2 value, and calculated the power saving in the same way as before:

The Zipp Super 9 rear disc wheel give the following benefits, both at 41.52kph:

                     Zwift Insider (75kg, 300W, 41.52kph)           Me (73kg, 270.6W, 41.52kph)

CdA              0.2710 -> 0.2685 (-0.0025 or -0.92%)      0.2415 -> 0.2390, (-0.0025 or -1.04%)

Power saving           2.5W saving (-0.83%)                               2.4W saving (-0.89%)

In summary, the Zipp Super 9 disc wheel will save me about two and a half watts at typical flat TT speeds.  This benefit is fairly small, but certainly not negligible.

Road Bike vs Gravel vs MTB speed test

How much slower is a gravel bike than a road bike, on the road? 

How much slower is a mountain bike than a gravel bike? 

These are the questions I tried to answer with a quick test I did yesterday afternoon.  The results were a little surprising... 

The Bikes

Road Bike

A road bike from Planet X.

It has 50mm deep carbon wheels. The tyres are fast road bike tyres: Continental GP5000s with latex inner tubes.

Tyres were inflated to 80 psi.

It weighs around 7kg.

Gravel Bike

A titanium cyclocross bike from Planet X.

It's fitted with fairly fast small-knobbed gravel tyres (hence I'm calling it the "gravel bike"). The tyres are 43mm Panaracer GravelKing SK TLCs, run tubeless.

Tyres were inflated to 25 psi.

It weighs around 9kg.

Mountain Bike

A Scott hardtail.

On the front, it's fitted with a 2.25" Schwalbe Rocket Ron Snakeskin Addix Speed tyre. On the back, it has a 2.2" Continental Race King Protection tyre. Both are tubeless. These are both fast XC tyres.

Tyres were inflated to 22 psi.

It weighs around 9kg.

Clothing / Kit

For all three bikes, I wore the same road bike style kit, a tight fitting jersey and lycra shorts, base layer, standard helmet.  The same two bottles were used on all of the bikes.

Test Method

I rode the same 8 mile road circuit on all three bike, back-to-back during a 2 hour window.  It was fairly flat, with only 80m of climbing over those 8 miles.  I started with the road bike, then the gravel bike, then the MTB.

I recorded the speed on 7.5 mile stretch that was fairly uninterrupted. There was one set of traffic lights, at mile 5, where I had to stop the Garmin and re-start it. My average speeds that I extracted from Strava are not affected by the length of the stoppage at the lights.  Speed and position data was from GPS.

I tried to ensure a consistent effort on all three bike.  The road and gravel bikes both have Stages power meters. My previously power meter cross-calibration work showed that my road bike power meter over-reads by about 10W relative to my gravel bike's power meter. Hence I targeted 250W for the road bike and 240W as the target for the gravel bike.

My mountain bike doesn't have a power meter, so I had to go off feel, targeting the same rate of perceived exertion as for the other two.  I did however, have a heart rate monitor, and although I wasn't monitoring my HR during the test, my HR was close between all three bikes (Road Bike:160bpm, Gravel:157bpm, MTB:156bpm).  As a result, I was fairly satisfied that my effort and power was similar on all three bikes.

The geometry and position on the bikes is obviously different.  I chose to ride all three bikes in the style and position I would normally chose for riding each of those bikes.  Therefore, for the road bike, I was most stretched out and had the lowest torso.  I was most upright for the MTB. For the gravel bike, I was in between the other two. 

Results

As mentioned in the intro, the results were a little surprising:

   Road Bike:   20.2 mph / 32.5 kph,  245W average

   Gravel Bike: 18.5 mph / 29.8 kph, 239W average (=249W with +10W correction)

   MTB:            18.6 mph / 29.9 kph

So the Gravel bike was 8.5% slower than the road bike, which is close to what I expected.  The real surprise, though, is how fast the MTB was relative to the other two, and that it was marginally faster than the gravel bike!

Analysis

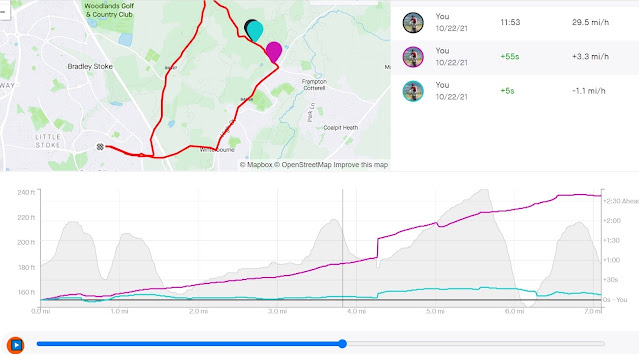
I created a segment in Strava, and used the Strava comparison feature to see how all three compared:

Gravel = Black (the reference), Road Bike = pinky purple, MTB = blue 

Looking at this plot, it's clear that the road bike gains time on the other two everywhere.  Ignore the steps at ~4.3 miles, which is the traffic lights.  Stopping at the traffic light affects the segment times, which is based on clock time, but it doesn't affect the average speed, because I stopped my Garmin and is therefore based on time moving.

Then, the plot shows the MTB seems to gain time slightly on the uphill sections and lose time on the downhill sections.  The time losses on the faster downhill sections make sense, because the MTB and my position on the MTB is obviously less aerodynamic than the other two bikes.

It was strange, though, that it gained time on the gravel bike on the slower uphill sections. The two are similar in their weight.  Could it be the rolling resistance? Both gravel and MTB tyres were reasonably fast tyres, but the gravel bike tyres look like they should be faster.

To check this, I looked at the rolling resistance data on the Bicycle Rolling Resistance website, which is an excellent resource that I use to help me choose tyres.  I was familiar with rolling resistance data for all my sets of tyres, versus alternative choices in their categories, but I'd never compared the rolling resistance of gravel and MTB tyres against each other. To my surprise, the MTB tyres are actually lower rolling resistance that the gravel tyres:

Gravel Tyres: 56.6W @27psi,  49.4W @36psi -> 65.4W at the 25psi pressure ridden

                         -8W adjustment for tubeless setup -> 57.4W at the 25psi pressure ridden

MTB Front tyre: 48.6W @35psi, 53.4W @25psi -> 59.6W at the 22psi pressure ridden

MTB Rear tyre: 36.0W @35psi, 40.4W @25psi -> 46.1W at the 22psi pressure ridden

MTB average: 52.8W assuming 50/50 front/rear weight split (for simplicity)

                         -10W adjustment for tubeless setup -> 42.8W at the 22psi pressure ridden

All power values above are for two tyres at 85kg load at 18mph, which is quite close to my test conditions.  The GravelKing tyre data was for 38mm version, but recent testing on the BicycleRollingResistance website has shown that the performance difference between 35mm and 40mm versions of the GravelKing TLC is very similar, so using the data from the 38mm version is good enough I think.  Both rolling resistance numbers have been adjusted based for tubeless a tubeless set-up, because the standard testing uses butyl inner tubes. The MTB tyre power number was reduced by 10W, based on this BicycleRollingResistance data.  The gravel tyre power number was reduced by an estimated 8W, estimated by looking at how latex tube versus butyl tubes affected the MTB and road bike power numbers.

Something to note is that I am running foam tyre inserts in my Gravel tyres, although I took care to ensure the tyre inserts are not contacting the tyre and getting compressed at the contact patch (and with some margin to spare), to ensure the tyre inserts don't affect rolling resistance.

For reference, the road bike tyres are much lower rolling resistance than both the gravel and MTB tyres:

Road Bike tyres: 20.0W for a GP5000 with latex tubes at 80 psi, i.e. a 23-37 Watt advantage over both the MTB and gravel bike tyres.

Discussion & Conclusion

The results surprised me, but upon closer inspection it's clear that the MTB has an (unexpected) 14.6 Watt rolling resistance advantage of the gravel bike.  This seems to have an beneficial effect at the slower speeds, when the aerodynamic disadvantages of the MTB are less dominant, and overall it gave the MTB a marginally higher speed one the 7.5 mile road route.

We have to keep in mind that the MTB did not have a power meter, but nevertheless I took care not to go 'too hard' on the MTB, by riding that bike last (when I was most fatigued), and by checking my heart rate data after the ride, to ensure it was not higher than for the other two bikes. 

This leads me to now wonder: If my gravel bike isn't faster than the MTB on a flat-ish road route, in what situation would the gravel bike be better than the MTB, if any?? 

Stiff pedal bearings/seals - What's the power loss?

 

The other day, one of my friends commented in our bike chat WhatsApp group about his flat pedals and how they were "quite stiff".  He was wondering how much power this would be costing him.

I told him that if he was curious enough to spend a few minutes looking into it, he could measure the resistive torque and calculate the associated power loss from that.

I did a back-of-the-envelope calculation of the power cost, based on 80 rpm cadence (see below).

The resistive torque he can feel when turns the pedals is either coming from either poor bearings, or more likely (as the pedals were new), from stiff seals.

I told him he could measure the resistive torque by hanging a weight off the pedal and measure the distance from the pedal axle.  Progressively adding weight until the pedal turned would then give a resistive torque (weight in Newtons multiplied by moment arm). Multiplying by cadence in rad/s then provided the power lost for one pedal.  Multiply by two to give total bike power loss.  Strictly speaking, what's measured with this method is stiction, or rather the resistive torque due to stiction, whereas we really want the friction losses when the pedal is turning. That's more difficult to measure simply though.  I think the stiction torque would give a conservative (slightly high) estimate of the power cost, which is good enough I think.

The results?  He found he needed 161g of weight at a 5cm moment arm to turn the pedal.  He calculated this to be 1.35 Watts of power loss using my equation below.  So not significant, but not nothing either.

Real life speeds versus virtual cycling speeds

 

I like the RGT Cycling virtual cycling app.  Unlike Zwift, it has a neat feature that allows you to create 'magic roads', which are virtual roads created from real road GPX data.  Anybody can upload GPX data to create a magic road.

This allows you to ride real roads inside RGT Cycling, so either local roads that you've ridden already, or famous roads that you'd like to ride (created by other people).

In this time of COVID-19 restrictions, it means that virtual races can be organised on real racing circuits, which is pretty cool.  Somebody else has already uploaded my local Odd Down Cycle Racing Circuit to the magicroads.org website.  Virtual races are being organised by PDQ Cycle Coaching, the guys that organised the real life races I did back in 2019.

The Odd Down Cycle Circuit is located near Bath, in the South West of England.  It's a 1-mile circuit, with very mild elevation changes and a couple of hairpins that can be taken at speeds below about 20-25 mph.

RGT Cycling also prides itself on providing a realistic virtual cycling simulation, which is something I like.  They strive to get the modelling accurate and the app includes features like braking and speed limits around tight corners, which is something that's different to Zwift, for example.

I thought it would be interesting to compare my real life cycling speeds around the Odd Down Circuit with the virtual speeds achieved in RGT Cycling.

Real life speeds

I extracted speeds from three races I did in Spring/Summer of 2019.  I only extracted speed from the warm up laps, not the races themselves, so that the speed would not be subject to drafting.  The average power during these warm ups varied from about 150W to 260W.  I usually do a ramp-type warm up, with the power held constant for 2-3 minutes at a time before increasing it. Therefore, most of the warm-up laps were done at roughly constant power.

The data from three separate warm ups (three different days) allowed some checking of the influence of external weather conditions, which would affect average speeds.  Lap speeds were obtained from Strava for the one-lap segment that has been created in Strava.  Results are shown below with blue symbols.

I also wanted to check my CdA because any speed discrepancies with RGT could be due to different CdA assumptions by RGT.  I estimated my CdA by loading my warm up GPX data into Golden Cheetah and using the Aerolab Chung method virtual elevation plots to determine CdA.  My CdA could be estimated for two of the three warm ups, and was 0.360 and 0.375 m^2 for those two warm ups.  I had to make some assumptions/guesses about the rolling resistance coefficient (CRR=0.004), the drivetrain efficiency (97%), my total weight (80kg) and the air density (1.2 kg/m3).  It's worth noting that my warm up laps were done on the hoods, with fairly straight arms, whereas my RGT avatar drops into a more aerodynamic horizontal forearm position when speeds are above about 25 kph (15 mph), which is most of the lap. 

RGT Virtual Speeds

I rode the Odd Down Circuit in RGT Cycling on Saturday 6th Feb 2021, selecting no bots, so that my riding would be solo, with no drafting.  The speeds were measured in the same way, using a Strava segment, and are shown with the red symbols on the plot above.  The RGT ride was also loaded into Golden Cheetah, making similar assumptions about CRR=0.004, drivetrain efficiency (97%), weight (80 kg) and air density (1.2 kg/m3).  This gave a CdA value of 0.285, which is quite a lot smaller that my real life CdA of 0.360-0.375.  Incidentally, I saw a tweet from Robert Chung a while ago, saying that he had found that Zwift also assumes a rather optimistic CdA of 0.28.

Differences and possible reasons

The general agreement in the plot above seems to be not too bad on the face of it, but it's not great either.  The RGT speeds are approximately 1-2 mph higher, and this I think comes primarily from the lower CdA assumed by RGT.  The difference of CdA, 0.285 in RGT versus 0.370 in real life, is quite significant.  That difference would result in a speed difference of 1mph at 250W, or about 30W at a fixed speed.

Of course, RGT is not trying to simulate me personally, and it has no idea how aerodynamic my bike and body combination is, or was during those warm ups.  It's worth bearing in mind that my warm up laps were done on the hoods with fairly straight arms, so that position will be less aerodynamic than what RGT is assuming.  I also wasn't wearing a skinsuit, and hadn't shaved my legs, both of which the RGT avatar has.  These are differences that Specialized have shown in their videos have a significant effect on aerodynamic efficiency.

It's also worth noting that I used the same power meter for all rides, including indoor RGT ride, so there should not be a bias coming from using different power meters.  It is possible that my left crank only power meter is slightly over-estimating my power, and there is some evidence of this based on recent testing.  An over-estimated power would result in RGT speeds that are higher than real life, and could also partially account for the different apparent CdA values. 

Overall though, I think the differences are primarily coming from the different riding position that RGT is assuming (horizontal forearms), relative to the position I adopted during my real life warm ups (almost straight arms, more upright torso).  Wind tunnel test performed by Aerocoach in 2019 showed that dropping the elbows into a horizontal forearm position ('breakaway hoods') significantly reduced Xavier Disley's CdA from 0.3506 m^2 to 0.2718 m^2.  This reduction of around 0.08 m^2 is very similar to the CdA differences extracted from my RGT ride and my real life rides, for similar changes in position.  Therefore, I conclude that the RGT cycling simulation is accurate, once you factor in the cycling positions that are assumed and adopted by the RGT avatar.

Besides this quantitative comparison of speeds, there is a qualitative element too, particularly around the cornering.  I found the RGT simulation of corners to be fairly realistic.  In real races, I usually have to brake for the hairpins due to the concertina effects when riding in the bunch.  During warm ups or solo breakaways, though, I often don't need to brake.  I remember holding about 280W during one solo breakaway and not needing to brake, although that was very close to the limit.  In RGT, the same thing happened, with just a momentary 1-2 seconds of braking before the bottom hairpin during the laps at 270W.  Qualitatively, this seemed to agree with real life, although it's difficult to be too conclusive.

Conclusion

All in all, I'd say that the RGT simulation is a realistic simulation of real life riding around my local Odd Down Cycle Circuit.  Where differences exist, I think there are some plausible explanations for what might be causing those discrepancies.  

 

Stages Power Meter Cross-Calibration

 

I recently bought a new Stages 3rd generation power meter (PM) for my new gravel bike.

This is the third power meter I now own, with the other two also being Stages PMs. The other two PMs I own are on my road bike and my time trial bike (a 1st gen and 2nd gen Stages PM respectively).

I decided to buy another Stages, partly because Stages PMs are good value for money (this third one was less than £300 brand new), and partly because I was keen to have the same brand of PM on all bikes.  My hope was that by having the same brand of PM, they would deliver consistent power values between the three devices.  However, I wanted to check how consistent they actually are...

Method

The best way to do this, I decided was to use my Wahoo Kickr Smart trainer as the 'balance'.  In general, the power numbers from smart trainers are not considered to be as accurate as those from dedicated power meters. However, with some care, the power values from the my Kickr smart trainer should at least be consistent, meaning that my Kickr could be used a common power source to enable the other devices to be compared with each other.  The agreement with the values from the Kickr is unimportant.

Some care was taken to ensure consistent testing of the three devices

• Testing was done in the same gear, 50t front, 16t cassette, and at the same cadence (85rpm)
• The same pedals and RH crank/chainrings were use for each PM test.
• All PMs were stored in the same place (same temperature) before installation.
• The Kickr smart trainer was connected via bluetooth to my iphone.  The power meter was connected with ANT+ to my Garmin Edge 520, to provide independent recording methods.
• Exactly the same PM installation sequence was done each time.
• The same testing protocol was done for each PM.

The protocol for the testing was as follows:

1. With no power meter installed, I warmed up the smart trainer for 15 minutes at 140-170 Watts.
2. The smart trainer was then calibrated. No further re-calibration of the trainer was done.

Then, for each of the three power meters, the following was done:

1. Install the first power meter. LH crank bolts tightened to 12Nm.
2. Power meter calibrated (zero offset) via the Stages app.
3. Collected power data at the first power setting, 150W:
• Use TrainerRoad app to set the smart trainer target power to 150W in ERG mode.
• Pedal for 1 minute to allow everything to stabilise.
• Press the lap button, and pedal for a further 2 minutes to collect power data.
• Record the average power from the power meter (Garmin) over the two minutes.
4. Collect power data at second power setting, 215W, using the same steps.
5. Collect power data at third power setting, 280W, using the same steps.
6. Optional: Collect repeat power data at 215W and 150W if time, energy, and motivation permit.

The order of testing the power meters was:

  1) Stages Shimano 105 7000 Gen 3 power meter

  2) Stages Shimano 105 5800 Gen 2 power meter

  3) Stages Shimano Ultegra 6700 Gen 1 power meter

4) A fourth run was done with a repeat of (1), the 105 7000 Gen 3 power meter, to check the repeatability after a PM re-installation.

Results

Repeatability

You can see from the plot above, that there's a fair amount of variation seen in the results, not just between the three power meters but also some significant changes seen in the repeats.  Ideally, the repeats should be very close to the first recordings, so what can we learn from this?

Starting with the repeats, the installation repeat run gave some differences of 2-11 Watts between run (1) and run (4) for the same power meter. There are several possible explanations for this difference that I can think of:

Explanation 1) The Stages power meter calibration drifted between runs 1 and 4.  This is unlikely because both runs were done with exactly the same protocol, so there is no additional usage of the PM that should cause a drift. For example, it was no warmer on the 4th run, having been inactive for 45-60 minutes.  Also, the differences between the powers are not consistent across the range, so it's not a parallel offset that would otherwise indicate a calibration drift.

Explanation 2)  The Wahoo Smart trainer has drifted.  Again, I think this is unlikely because if this were true, I'd again expect a constant parallel offset to be seen between runs 1 and 4.

Explanation 3) The most likely hypothesis is, I think, that both runs are subject to small changes in my left/right leg balance, with random changes affecting the results.  For example, if at 150W I have a 48/52% left/right leg split, then the left leg produces 72W, the right leg produces 78W to create the 150W (real) power total. However, the Stages PM always assumes the right leg also produces the same as the left, 72W, so the Stages PM would give a total power of 144W. If that L/R balance then swings by 4% to 52/48% L/R instead, then the left leg produces 78W, the right leg produces 72W, but the Stages PM gives a total power of 156W.  So a swing of 2% asymmetry to the left, to 2% assymmetry to the right, will create an apparent power difference of 12W for the same actual 150W power total in both cases.  If the target power is higher, say 280W, that same swing would be higher, 22.4W.

I think this is third explanation, of random small changes to the L/R leg imbalance, is the most plausible explanation of the 2-11 Watt variation seen in the installation repeat. It also explains why similarly large differences are seen in the repeats that were done before uninstalling each power meter (step 6 in the method).

Power meter differences

The differences between the power meter results has to be considered with a view of these repeatability results.  However, even considering the repeatability, and the uncertainty that it introduces, I feel the Gen 2 105 power meter (the red data points) is reading higher that the other two PMs.  Although its difficult to be conclusive, I would say the the Gen 2 105 PM is reading around 10-Watts higher than the other two.

This isn't a huge difference, but it is large enough that I'll need to take it into consideration when riding close to my limit, close to threshold.  This Gen 3 105 PM will go onto my gravel bike, with the Gen 2 staying on my Road bike, which I use for most training, FTP tests etc.  I will therefore have to keep in mind that the power values on my gravel bike may read a little low compared with what I am used to on my road bike, for the same effort level. 

The importance (or not) of rotating weight on a bike

In short: It's not!  Any extra rotating weight (or reduction of rotating weight) is, at the most, twice as important as non-rotating weight. And even then, this factor only applies to situations when you're accelerating.

The first piece of bike-related engineering analysis I ever did was back in 1994.  I wanted to include it here, for posterity.

I had just started an internship, during the 3rd year of my Engineering degree. I was doing my internship at a British company called the DRA (the Defence Research Agency).  This was a government funded organisation that performed aeronautical and other defence-related research on behalf of the UK government and industry.  It was the UK's equivalent of Germany's DLR, France's ONERA, or America's NASA.

I wasn't into cycling much at this time, but I shared an office with a guy called Gerry, who was himself a keen cyclist in his 30s.  Among the many conversations that we had, one time he got onto the subject of rotating weight on bicycles.  He explained that any weight savings on rotating components, such as wheels and cranksets were "much much more important" than weight savings elsewhere on the bike.

Many people will recognise this is an assertion that cycling enthusiasts been pushing for many years.  Thankfully this myth has now been largely debunked.  However, back in 1994, upon hearing this claim I had no access to the internet or any means to check or disprove what Gerry was telling me.

I was suspicious about his assertion, though, it didn't feel right.  So I decided to look at the equations governing rotating weight and energy, in order to decide for myself how important rotating weight is.  I don’t have my notes from back then, unfortunately, but I’ve recreated them below.

The basis for this assertion about rotating weight importance is that for non-rotating components, any additional mass is only subject to linear (translational) acceleration, when the bike/rider system is accelerated. On the other hand, any additional mass on a rotating component, such as a wheel, is subject to both linear acceleration and rotational acceleration.  Proponents of the “rotating weight is important” idea believe that the rotational energy needed to 'spin up' this additional mass is significant, several times more significant than the energy needed to linearly accelerate and create the purely translational kinetic energy of a non-rotating component.

We need to examine this idea of additional rotating mass having a significant amount of rotational energy, relative to a non rotating mass, which has only linear kinetic energy when it is accelerated. 

The equations below show how the two scenarios compare: How the total energy compares between a situation where the additional mass is rotating, compared with a situation where the additional mass is non-rotating.

Equation #1 below describes the reference situation, defining the total energy of a bike and rider that has accelerated from rest to velocity V.  Equation #2 describes the same bike and rider that has accelerated again to velocity V, but with an additional non-rotating weight dm.  Finally, Equation #3 describes the same bike and rider, but this time the additional weight dm is on a wheel at a radius r from the hub. The radius of the wheel+tyre is R.

The incremental effect of the rotating component of the additional weight is therefore defined by the difference between equations #2 and #3.  Instead of having an additional energy term of 0.5*V^2*dm for the non-rotating weight, when the extra weight is on the wheel the additional energy term is 0.5*V^2*dm + 0.5*V^2*dm*r^2/R^2.  Therefore, the situation with the rotating weight has more energy than the non-rotating extra weight case by an amount equal to 0.5*V^2*dm*r^2/R^2.

The extra energy therefore depends on the location of the extra weight.  If the extra weight is near the axle (r/R is zero or very small), the rotating element of the extra weight is negligible, because the moment of inertia associated with it is negligible.  In the opposite case, if the extra weight is close to R, i.e. in the tyre, tube or rim, then the rotating element of the extra weight becomes 0.5*V^2*dm, because r/R=1.  In other words, if the extra weight is in the tyre or rim it is twice as important as having the weight on a non-rotating component.

That's the maximum amount possible; twice as important.  Remember also that this extra energy only makes a difference during an acceleration.  At a steady speed instead, such as steady climb up a hill, there is no acceleration, therefore it doesn't matter whether the extra weight (or weight saving) is on a rotating component or a non-rotating component.