Bike upgrades - Which offer the best value for money?

I did this analysis in 2016.  In fact, it was the first significant piece of bicycle performance analysis that I did, or at least, it’s the first study that's worth writing about.  The objective was to calculate which road bike upgrades offered the best value for money, in terms of making me faster on the bike.

I have been a keen cyclist for years, since about 1994 when I bought my first bike, a cheap £200 mountain bike.  In those first 15-20 years of recreational cycling, I frequently upgraded my bike(s) with new and better components. Like many other people during that era, I focussed on making my bikes lighter.  I was a bit of a weight weenie in those days, I'm ashamed to say.  Sadly, I can’t even say that my fitness justified the attention to detail that I put into my bike upgrades.

In the winter of 2015/2016, I realized that I knew everything necessary to model the forces and power losses that occur when riding a bike, and I was therefore able to analyse and quantify how much benefit could be achieved by making various improvements to either the bike, the kit or it's rider.  Doing so would mean that I had the possibility to check how beneficial all those weight savings had been on my cycling performance and how beneficial other types of improvement would be.  In turns out that I was in for a bit of a shock...

Method

My previous blog post explains the Excel-based method I created to model the power required to propel a bicycle at a certain speed and for certain set of conditions. That performance model development was a precursor to the analysis described in this post.  The Excel-based performance model also allows the power delivery/speed profile to be optimised for a prescribed cycle route (i.e. a gradient profile).  This optimisation functionality is important, because changes in bike equipment might lead to a slightly different optimised power profile that achieves the fastest bike speed (or in terms of how the actual computation is done, a slightly different optimised speed profile that achieves the prescribed average/normalised power constraint).

Re-optimisation example

The example below illustrates this, for a case where 2 kg is removed from the bike weight.

Case 1 in the table below is the optimised power profile for a 80km route described in the previous blog post, with the speed profile optimised to maximise the average speed (i.e. minimise ride time) for a prescribed normalised power of 200W.  In case 2, the weight is reduced by 2 kg, but the same speed profile is maintained. This results in a reduced normalised power of 197.294W, so a saving of about 3W (i.e. 2kg weight saving gives a 3W saving at the same speed).  For case 3, the same 197.294W normalised power is used as a constraint, and the speed/power profile is re-optimised.  This gives a small 3.6 second time improvement.

Although this re-optimisation change is very small, I wanted to do the power profile re-optimisation for each bike modification analysed to provide the best like-for-like comparison.  I also couldn't be sure that some bike modifications wouldn't affect more significantly the optimised power/speed profile.  I also think it's more relevant to know the speed improvement associated with a modification, for a fixed power, rather than a power improvement, since we tend to ride at a given power target/limit (our maximum capability) instead of targeting speed. The speed improvement is only achieved in my Excel model by re-running the optimisation.

                                     Bike weight        Avg Power       Normalised Power       Time           NP improvement

1) Optimised Power                 7 kg                192.6 W                 200.0 W         2 hrs 51.11 mins                -

2) Same speed profile as 1     5 kg                191.7 W                 197.3 W         2 hrs 51.11 mins             -2.7 W

3) Optimised speed profile     5 kg                191.7 W                 197.3 W         2 hrs 51.05 mins             -2.7 W

Bike modifications analysed

For the modifications I analysed, I considered a range of changes to the bike that would affect one of the forces of resistance acting on a bicycle:

• Aerodynamic resistance - Expressed via the CdA value (drag coefficient multiplied by frontal area) in the model. Items like aerodynamic helmets, deep section wheels, skinsuits etc.
• Rolling resistance - Expressed via the CRR (rolling resistance coefficient) value. Items like cheap versus expensive tyres, mountain bike tyres versus road tyres, inner tubes etc.
• Weight effects - Generally only affect the bike performance when riding uphill, but there is also a very small effect on rolling resistance on the flat too. 

In addition, I also looked at power changes, which would come from fitness improvements.  Again, the objective of all this was to understand relative differences between these changes.

Data sources

At this point, it's worth mentioning where I got my data from:

• For aerodynamic changes, I reverse-engineered the 40km time savings quoted by Specialized in their Wind Tunnel YouTube series.  I did this by iteratively determining the CdA reductions in my model needed to achieve the 40km time savings that the guys at Specialized quote.
• For rolling resistance changes, I took data from bicyclerollingresistance.com.
• For weight changes, although most changes were arbitrary changes like 1kg or 5kg reductions, I equated this to tangible changes like the cost of buying a more expensive groupset by looking at price data on Wiggle and weight data from bike component manufacturers such as Shimano.  For example, a Ultegra grouset will cost around £400-500 more than a 105 groupset, but will save around 200-300g.

Routes considered for analysis

I considered the same three fictional routes that I described in my previous post. Most of the items were analysed for Route 1, which is typical of many medium length sportives that might be done in the UK.  Results for routes 2 and 3 give some indication how sensitive the results are to the amount of climbing, which can be interesting because, for example, the effects of weight reductions on flat routes are almost negligible.

Route 1: Typical short/medium sportive - 80km route, 1000m of climbing, 200W normalised power.

Route 2: 40km TT - 40km perfectly flat route, 250W normalised power.

Route 3: Hilly route: 40km route with 900m of climbing, 250W normalised power

Baselines values

The various modifications analysed were considered relative to the following set of reference conditions:

• Air pressure = 1012.5 mbar (i.e. International Atmosphere sea level pressure)
• Air temperature = 20 degrees C
• Air density = 1.203 kg/m3 (calculated from the above pressure and temperature)
• Bike weight = 7kg
• Rider Weight = 11st 7lbs (161 lbs or 73.2kg)
• CRR = 0.045
• CdA = 0.36 m^2

Results

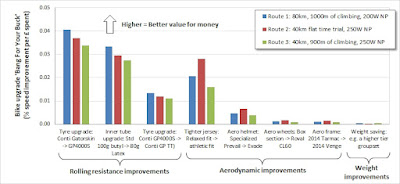
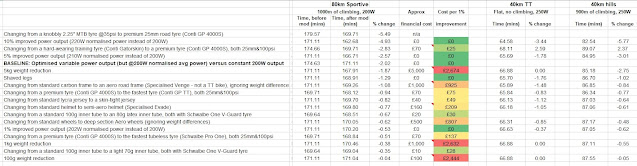
The table below shows the results for a number of bike modifications, with percentage time improvements ("% change" column) calculated either relative to the baseline setup above, or versus a degraded setup.

The cost effectiveness column called "cost per 1%" shows which modifications offer the best ride time improvement (or average speed improvement) for the money.  Green and yellow boxes show the best value for money modifications, whereas red items are poor value for money.

Improvements and cost effectiveness of various bike modifications

 There are a few key takeaways from this study:

• Power improvements: If you can improve your power, through improved training etc, at no extra cost then that is a very effective way to improve your average speed. For the 80km route, a 5% power improvement gives a 2.57% speed improvement.

• Optimised power: As discussed in my previous blog post, even if you are not any fitter, applying more or less power at the right time (i.e. optimising your power delivery) gives a significant 2.02% average speed improvement versus a constant power approach, even though the normalised power is no different.

• Rolling resistance improvements: By far, the best value for money upgrade you can make to a bike is improvements to your tyres and tubes.  Upgrading tyres and tubes will typically provide a cost effectiveness in the region of £30 per 1% improvement.  Even if you start from good tyres, like Conti GP 4000s tyres, upgrading to the best tyres is still less than £100 per 1% improvement.

• Weight: On the other hand, buying expensive components that will make your bike lighter are extremely poor value for money.  I have used the assumption of £1 per gram saved, which is a typical price you'll pay when going for a next tier groupset for example such as buying Dura Ace instead of Ultegra.  Spending £1000 to save 1kg will improve you average speed by only 0.38%, so that's around £2000-£3000 per 1% improvement!

• Aerodynamic improvements: The value for money of aero improvements is in the middle, with aero wheels and aero frames being quite costly, per 1% improvement, but aero helmets being a more cost effect upgrade.  Getting a tighter fitting jersey is a very cost effective improvement, rivalling the tyre and tube upgrades in terms of bang for your buck.

The numbers in the table above are a little difficult to read, admittedly, so I pulled a few of them into the chart to show visually how certain improvements are significantly better than others, in terms of value for money:

From this chart, it's clear that buying upgrades to improve rolling resistance is money well spent.  The aero improvements shown all give broadly similar average speed improvements in absolute terms, as said in the Specialized video with their time-saving-over-40km metric.  However, buying a tighter fitting jersey will be about one tenth the price of aero wheels or a new bike frame, so clearly a tight fitting jersey represents much better value for money.

As for weight improvements?  Well, since the bars on the right hand side of the bar chart are barely visible, spending money to make your bike lighter is extremely poor value for money, when it comes to actually going faster.  It seems that all the money I spent on lightweight components for many years was, sadly, a unwise choice.

Trades

It's finally worth showing some 'trades', i.e. what changes are equivalent, in terms of the resulting bike speed improvement.  These values have been obtained from the results above and their associated changes to either power, weight, drag or rolling resistance.

A 1% speed increase is achieved by:

Either a...   1.95% power increase

     Or a...    0.00077 CRR reduction

     Or a...    0.0153 m^2 CdA reduction (=4.3% CdA reduction)

     Or a...    2.67 kg weight reduction

 

Conclusion

In summary, spend your money on fast tyres and tubes as a priority, then upgrade to a tight fitting jersey.  For around £150, buying fast tyres, latex tubes and a tight jersey could improve your speed by 4-5%, depending on your starting point.  On the other hand £150 spent on lightweight components won't even improve your speed by 0.1%!

Finally, improving your power output, either by getting fitter to raise your power, or by optimising your power delivery, is a very effective way of going faster on the bike.

What’s the fastest way to ride a cycling route?

This was was the first piece of cycling performance analysis that I did, back in 2016.  A few months before that, in late 2015, I had bought a power meter for my road bike.  I really liked the data that it provided, allowing me to pace my rides with more precision.  I quickly began to question, though, how should I pace a ride to achieve the fastest time, i.e. the highest average speed?  Should I try to keep my power constant, regardless of the terrain and wind conditions, or would it be quicker to increase the power on some sections of the route?  We often hear that for time trials the fastest time is achieved by holding the highest possible fixed power, instead of going 'too hard' at the start.  However, most time trials are held on flat routes, and I had a feeling that the constant power approach may not be best for hilly routes.

This is question is essentially an optimisation problem: What is the optimal way to deliver the power to minimise ride time (i.e. maximise average speed) for a set of constraints.  I decided to see whether Microsoft Excel's built-in optimiser could solve this kind of optimisation problem.

I should point out that, at this time, I wasn't aware of BestBikeSplit.com.  A couple of years after I did this work I heard about BestBikeSplit on the TrainerRoad podcast and discovered that it does something very similar to my Excel spreadsheet, albeit in a slicker commercial package.  In fact, I'm not sure which year BestBikeSplit was originally developed, but I wasn't aware of it when I developed this Excel-based bike power optimiser.  A future blog post will show comparisons between my my Excel optimiser and BestBikeSplit, showing that they both give similar optimisation results.

Bicycle Power Modelling

The starting point of my Excel based power optimiser was to build a model that calculates the required power to propel a bike.  The equations of motion that describe the forces on a bike, and hence the power required to move it, are shown below.

This is another situation where I derived something myself, the equations below, and then some years later discovered that this model of the forces acting on a bicycle had been derived previously (not surprisingly). See here for Jim Martin's paper.

Power = (Fa + Fg + Fr + Fi)*V

   Where:

   Fa = Aerodynamic drag force (N)
   Fg = Gravitational component force (N)
   Fr = Rolling resistance force (N)
   Fi = Inertia force (N)
   V = Velocity (m/s)

   and:

   CdA = Drag area of the bike+rider (m^2)

   Cr = Coefficient of rolling resistance
   rho = Air density (kg/m^3)
   m = Mass of bike+rider (kg)
   t = time (s)
  g = Acceleration due to gravity (=9.81m/s^2)  

This power model was validated by comparing the power predicted by this model against the measured powers that I recorded during three Strava segments; 2 flat segments and an uphill segment:

1) Weston Hill, near Bath, South West England:

https://www.strava.com/segments/6665281 : 1.578 km, 10.3% gradient.

Real life: 18/07/15, 7 mins 35 secs (8.0 mph),  20 degC,  80.6 kg, 313 W average power

Model:  8.0 mph gives a power requirement of 314W using CdA=0.36m^2, Cr=0.0045

-> +1W (+0.3%) discrepancy

2) U102 out and back time trial segments, near Bristol: 

https://www.strava.com/segments/1286195?filter=overall : 5.60 km, -0.1% gradient.

Real life: 18/08/15, 8 mins 32 secs (24.5mph),  17 degC,  80 kg, 2 mph estimated tailwind, 267 W average power

Model:  24.5 mph (with 2 mph tailwind) gives a power requirement of 273 W using CdA=0.36m^2, Cr=0.0045

-> +6W (+2.2%) discrepancy

https://www.strava.com/segments/4769147?filter=overall : 7.42 km, 0.0% gradient.

Real life: 18/08/15, 13 mins 1 secs (21.3mph),  17 degC,  80 kg, 2 mph estimated headwind, 267 W average power

Model:  21.3 mph (with 2mph headwind) gives a power requirement of 260W using CdA=0.36m^2, Cr=0.0045

-> -7W (-2.7 %) discrepancy

The agreement between the model and measured (real life) powers agree within a few percent.  For the hilly segment, the model predicts the power requirement very well (a 1W or 0.3% discrepancy).  For the two flat segments, the model overpredicts the power requirement for the 'out' leg of the TT course and and underpredicts it for the return leg, due to the estimated wind effects.  If I were to tweak the headwind by just 0.3 mph (bearing in mind that I had to guess the headwind speed of 2 mph) then the model is spot on, within a few tenths of a percent for both out and return legs. Therefore, it can be concluded that overall the model and the values selected for CdA and Crr (drag area and coefficient of rolling resistance, 0.36m^2 and 0.0045 respectively) accurately simulate real life riding.

This model validation step was an important precursor to any subsequent use of the model for further investigations, as described in the next section.

Optimal power delivery

My Excel-based power model simulates a bike ride by splitting it up into several 'segments'. For each segment, which has a specified distance and gradient, the speed is set either by the user or by the Excel optimiser.  Then, the model calculates the power for each segment for the chosen speeds, assuming steady-state conditions.  Essentially, this neglects speed and acceleration transients between segments, which I understand is the same assumption made also by BestBikeSplit.

The powers for all of the segments can be time-averaged to calculate the overall average power for the ride, and this is the result that the optimiser is trying to minimise (or to look at it another way, it tries to maximise the average speed for a fixed average power).

I also included an approximate estimate for normalised power, since it's often that case that normalised power is the metric that we want to minimise or control instead of average power, to reflect the physiological cost of the ride.  My spreadsheet calculates only approximate normalised power though, because instead of using the 30-second average power to derive normalised power, it effectively uses 1-second power.  This is not too much of an issue, though, because most segments I used for these studies were much longer than 30 seconds, so there were no short segments where the time would be less that 30 seconds, where the normalised power calculation would have been significantly impacted.  Therefore, the approximate calculation of normalised power is fit for purpose.

The optimiser can be used to either target an average power number or a normalised power number, whichever is preferred.  In the subsequent example I chose to target a given normalised power.

Routes for optimiser

I created three fictional routes, to see how the optimised power would differ for different types of rides:

Route 1: Typical short/medium sportive - 80km route, 1000m of climbing, 200W normalised power.

Route 2: 40km TT - 40km perfectly flat route, 250W normalised power.

Route 3: Hilly route: 40km route with 900m of climbing, 250W normalised power

The profile for Route 1 (80km, 1000m of climbing) is shown below:

The profile for Route 3 (40km, 900m of climbing) is shown below:

Results: Constant power versus optimised power

For Route 1 (80km, 1000m climbing), the optimised power profile, targeting 200W normalised power is shown below (upper chart), compared with the fixed power profile (lower chart).  It is clear the that optimiser has determined that it is optimal to increase the power when ascending hills and reduce the power when descending hills.

                                 Average Power        Normalised Power             Time                  Improvement

Constant Power                  200.0 W                     200.0 W                 2 hrs 54.6 mins                  -

Optimised Power                192.6 W                     200.0 W                 2 hrs 51.1 mins                2.0%

An optimised power delivery achieves a 2.0% improvement (three and a half minutes) for the same normalised power of 200W.  Note that the same normalised power means the optimised power delivery has a 7.4W lower average power, at 192.6W.  Since it has the same normalised power and a lower average power, the optimised power profile would I think not only be faster, but would feel similar or easier than the constant power profile.

For Route 2 (40km, perfectly flat route), the optimised power profile, targeting 250W normalised power is exactly the same as the constant power profile, i.e. it is optimal to ride at at a fixed power of 250W.  This is not surprising, because the optimum power profile is a result of changes to the riding conditions. No changes in terrain or wind mean the optimum is a constant power profile.  If the terrain or wind were to change along the route, the optimal power at any particular point in a ride would change also, as can be seen for Route 1 above and Route 3 below.

For Route 3 (Hilly route: 40km route with 900m of climbing), the optimised power profile, targeting 250W normalised power is shown below (upper chart), compared with the fixed power profile (lower chart).  As for Route 1, the optimiser has again determined that it is optimal to increase the power when ascending hills and reduce the power when descending hills.

                                 Average Power        Normalised Power              Time                  Improvement

Constant Power                  250.0 W                     250.0 W                 1 hr 30.0 mins                  -

Optimised Power                237.5 W                     250.0 W                 1 hr 27.6 mins                2.7%

'Too hard' power                 224.7 W                     250.0 W                 1 hr 28.0 mins                2.2%

As for Route 1, the optimised power delivery achieves a significant improvement for the same normalised power.  In this case, the improvement is slightly more than for Route 1, at 2.7%.  Again, this improvement is achieved by pushing slightly harder on the climbs and then backing off slightly on the descents.

What happens, though, if you push even harder on the hills (labelled the "Too hard" case above)?  I took the optimised power profile shown in the plot above and increased the amplitude of the speed variation (fixed power versus optimised power) by 50%, then made a 0.2 mph global adjustment to the speed to keep the normalised power at exactly 250W.  For example, for the steep 10% gradient climb in the middle of the route, the climb is done at 6.64 mph for the constant 250W power profile,  7.48 mph at the optimum power of 283W, and 7.72 mph at the 'too hard' power of 293W.

The overall result is a ride time that's still better than the constant power approach, but is worse than for the optimum power profile. This also is a useful quick-and-dirty check that the optimiser is working as intended.  The very subtle differences in the chosen powers for the 'optimum' and 'too hard' power profiles (283W vs 293W) shows that it's difficult to select the optimum power based on guesswork alone, and it's easy to go too hard on hills. Anecdotally, this is something I see a lot of recreational riders doing on sportives, riding overly hard on the climbs.

Conclusion

My Excel-based power optimiser uses fairly simple modelling of the forces acting on a bike to estimate the required power for a given speed. This model has been validated based on real-life rides and measured power data.

The optimiser can determine the optimum (best) use of a person's power for any cycle route. The results show that improvement in time and average speed can be made by pushing harder (above average or normalised power) on the climbs and easing off on the descents (below avg or normalised power). This tends to be what riders do naturally when riding, but the optimisatiosn studies have also shown that it's difficult to judge how much harder and easier those power variations should be to achieve the best (optimum) ride.

The optimum power profile provides a significant performance improvement compared with a constant power approach.  2-3% improvements are possible, which may not sound like large improvements, but a 2-3% improvement is equivalent to about 5% power improvement, or a huge 5-6kg weight saving*.

* A future blog post will show these effects and the best way to spend your money on bike improvements.  In fact, this power optimisation model was a precursor for doing those best-bang-for-your-buck studies.

Finally:  Observant people will notice that that my power modelling doesn't have a correction for transmission losses, so it implicitly models a perfectly efficient transmission, or the power required at the rear hub, not power at the pedals. This was an oversight on my part. However, although it will affect the absolute predicted powers/speeds and therefore the CdA and CRR tuning, I don't believe it will affect the overall conclusions of this study.